Verlet Rope
So inspired by this tweet I made this thing:
I was curious about the technique, and as it sounded a bunch simpler than I'd imagined I couldn't help but try implementing it. A bunch of people have asked about the technique involved, and, while it's fairly simple I don't think I could fit into into a tweet, so this is a short explanation.
It's not a full how-to tutorial, sorry. I wouldn't rule out writing one in future, but this is not it, sorry.
Verlet Integration
The key thing that I hadn't heard of before was Verlet Integration. Now, I'm not the best person to talk authoritatively about maths but my layman interpretation is this:
Instead of using the familiar Euler method of calculating an object's position taking a velocity:
position = position + velocity
You can instead replace the 'velocity' part with the difference between an object's current position and it's previous position:
position = position + (position - old_position)
You can still achieve acceleration, by pushing the position away from old_position, but you cease to store a velocity for an object at all. Otherwise this is reasonably intuitive, but has some nice traits for games that were new to me.
Contraints
The reason Verlet Integration works well here is because using it, you can handle contraints surprisingly easily. Constraints here means both collision with the circles and the binding force between segments of the rope.
Instead of working out what the effect on velocity a constraint will have, all you need to do is detect that a constraint is breached, and move the object/s so that it is no longer breached. The velocity change of the interaction is handled, as if magically, because of the way you are storing velocity as position.
If you have a good deal of contraints you probably want to run this step over all your constraints many times every frame, to make the simulation more stable.
Rope
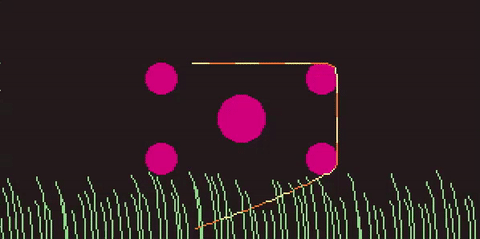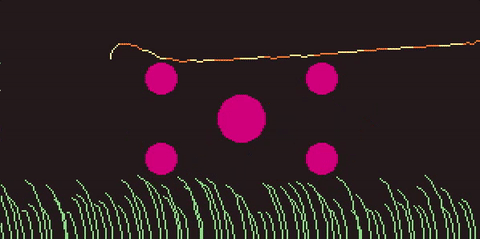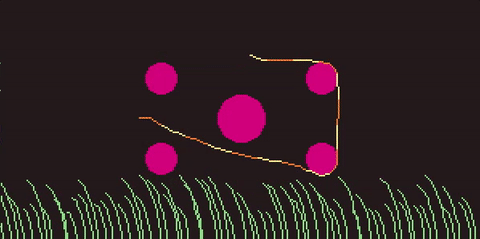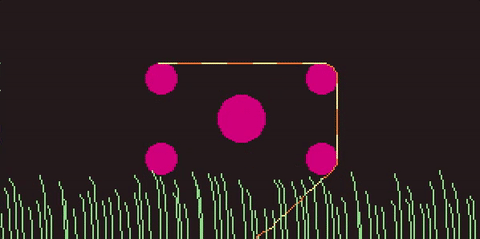
To make the 'rope' or 'snake' I simulate a whole bunch (64) points using verlet integration. Each of these has constraints to keep them outside of the circles, but also to ensure that the distance between a point and the next point on the rope remains constant.
The rope is controlled by, each frame, setting the position of a point at one end of the rope to the position of the mouse cursor. The rest of the points are pulled along behind it, springing forward to keep up and narrow the gap, satifying their contraints.
Remarkably, that (and a bunch of tweaking values till they feel right) is all that's required for a fairly stable and fluid feeling simulation.
Who Wrote This?
This guide was written by Jonathan Whiting. Thanks again to Thomas Bowker for the inspiration.
